Accepted Paper: A volume-averaged nodal projection method for the Reissner-Mindlin plate model

• Post by: alejandro
• July 31, 2018
• Comments off

Paper Accepted for Publication in Computer Methods in Applied Mechanics and Engineering

A. Ortiz-Bernardin, Philip Köbrich, Jack S. Hale, Edgardo Olate-Sanzana, Stéphane P. A. Bordas, Sundararajan Natarajan, “A volume-averaged nodal projection method for the Reissner-Mindlin plate model.”

ABSTRACT

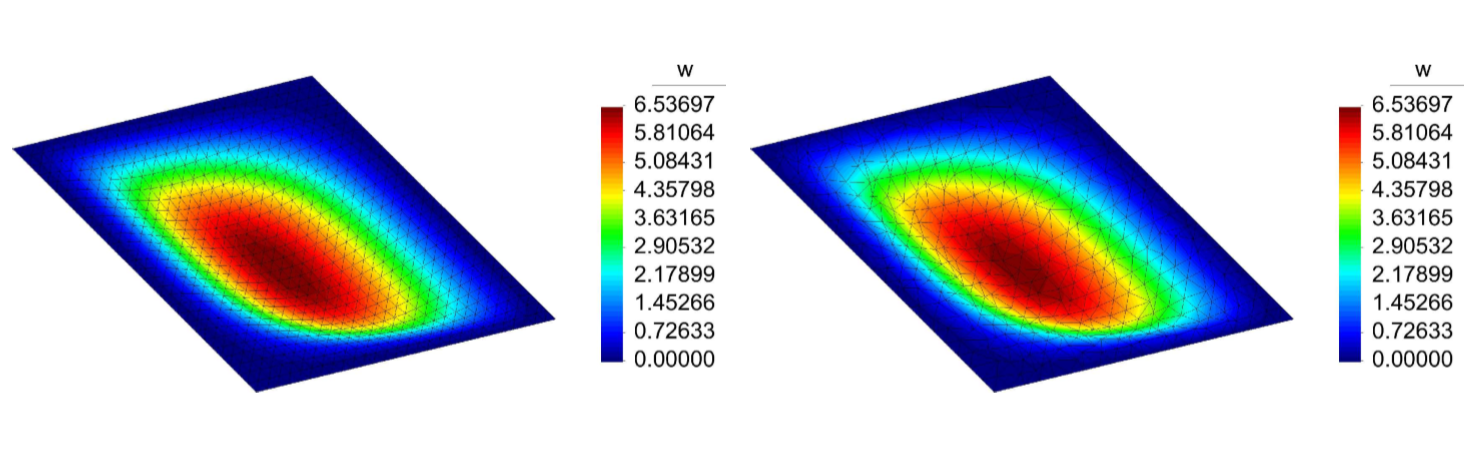
We introduce a novel meshfree Galerkin method for the solution of Reissner-Mindlin plate problems that is written in terms of the primitive variables only (i.e., rotations and transverse displacement) and is devoid of shear-locking. The proposed approach uses linear maximum-entropy approximations and is built variationally on a two-field potential energy functional wherein the shear strain, written in terms of the primitive variables, is computed via a volume-averaged nodal projection operator that is constructed from the Kirchhoff constraint of the three-field mixed weak form. The stability of the method is rendered by adding bubble-like enrichment to the rotation degrees of freedom. Some benchmark problems are presented to demonstrate the accuracy and performance of the proposed method for a wide range of plate thicknesses.

Keywords: meshfree methods; maximum-entropy approximation; Reissner-Mindlin plate; shear-locking; VANP method.