A MINI element over star convex polytopes

• Post by: alejandro
• December 10, 2019
• Comments off

Finite Elements in Analysis and Design
Vol. 172, pp. 103368, 2020

A. Francis, A. Ortiz-Bernardin, S. P. A. Bordas, S. Natarajan

Abstract

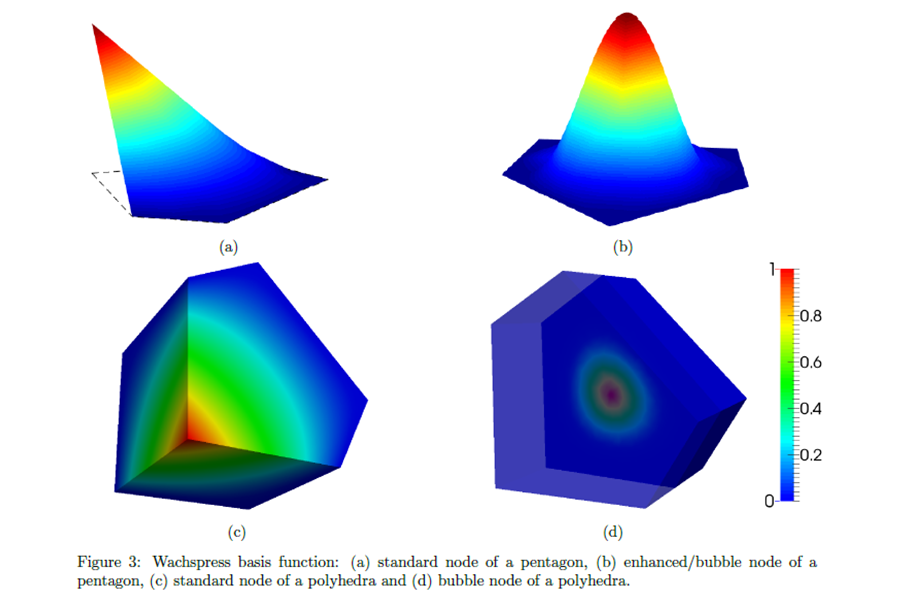
In this paper, we extend the concept of MINI element over triangles to star convex arbitrary polytopes. This is achieved by employing the volume averaged nodal projection (VANP) method over polytopes in combination with the strain smoothing technique. Within this framework, the dilatation strain is projected onto the linear approximation space, thus resulting in a purely displacement based formulation. The stability is ensured by enhancing the displacement field with bubble basis functions. The salient features of the proposed method are two fold: the VANP alleviates the locking phenomenon and the strain smoothing suppresses the need to compute the derivative of the basis functions, thus reducing the computational burden. Various benchmark problems in two and three dimensions are numerically solved to demonstrate the robustness, accuracy and the convergence properties of the proposed framework.

Keywords: VANP operator, nearly-incompressible elasticity, bubble basis functions, strain smoothing (SFEM), arbitrary polytopes, volumetric locking.

Original Journal Article: https://doi.org/10.1016/j.finel.2019.103368

Personal preprint: 

NOTICE: this is the author’s version of a work that was accepted for publication. Changes resulting from the publishing process, such as peer review, editing, corrections, structural formatting, and other quality control mechanisms may not be reflected in this document.