Paper Accepted: A Finite Element Formulation for Stressed Bodies With Continuous Distribution of Edge Dislocations

• Post by: alejandro
• April 13, 2015
• Comments off

Paper Accepted for Publication in Acta Mechanica

A. Ortiz-Bernardin, D. Sfyris, ”A finite element formulation for stressed bodies with continuous distribution of edge dislocations.”

ABSTRACT

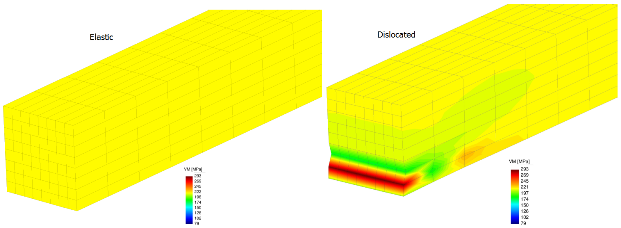
On using Noll’s theory of materially uniform but inhomogeneous bodies, a nonlinear finite element method for treating a body with a continuous distribution of edge dislocations is presented. To this end, we use the multiplicative decomposition of the deformation gradient, which is herein referred to as the F* decomposition. The nonlinear finite element method is devised starting from a hyperelastic-like strain energy as a function of F*. By making a specific assumption for the uniform reference, we model a bar with a continuous distribution of edge dislocations parallel to the plane that defines a cross section of the bar and with the Burgers vector along the axial direction of the bar. This body is subjected to pure tension along its axial direction and we examine how the presence of the defects affects the elastic solution. The numerical results are juxtaposed with the analogous ones that are obtained from the corresponding elastic material. It appears that the field of the defects affects the nonlinearity in the stress-strain response in the sense that stresses grow “faster” pointwise in the dislocated body. Thus, if a definite yield limit exists it is approached faster by the dislocated model at hand due to the presence of defects in the as-received body.

We also focus our attention in the case of only one dislocation and conclude that near the core region our model predicts finite stresses. Finally, a close loop consisting of a screw and an edge segment is treated within this theory. As expected, it appears that near the loop stresses are concentrated. Our framework is valid for a body with a frozen distribution of dislocations, namely, the defects exist but are not allowed to move. So, essentially, it models an elastic body with internal stresses resulting from dislocations. Thus, our approach is assumed to be one step before the initiation of plasticity and we are interested in how the field of the inhomogeneity that arises from a fixed distribution of defects affects the elastic solution. This is the first attempt to apply the multiplicative decomposition to problems with dislocations in the literature, thereby highlighting that Noll’s abstract approach can be put into the perspective of standard engineering computations.

Keywords: Materially uniform; inhomogeneous body; multiplicative decomposition; nonlinear finite elements.