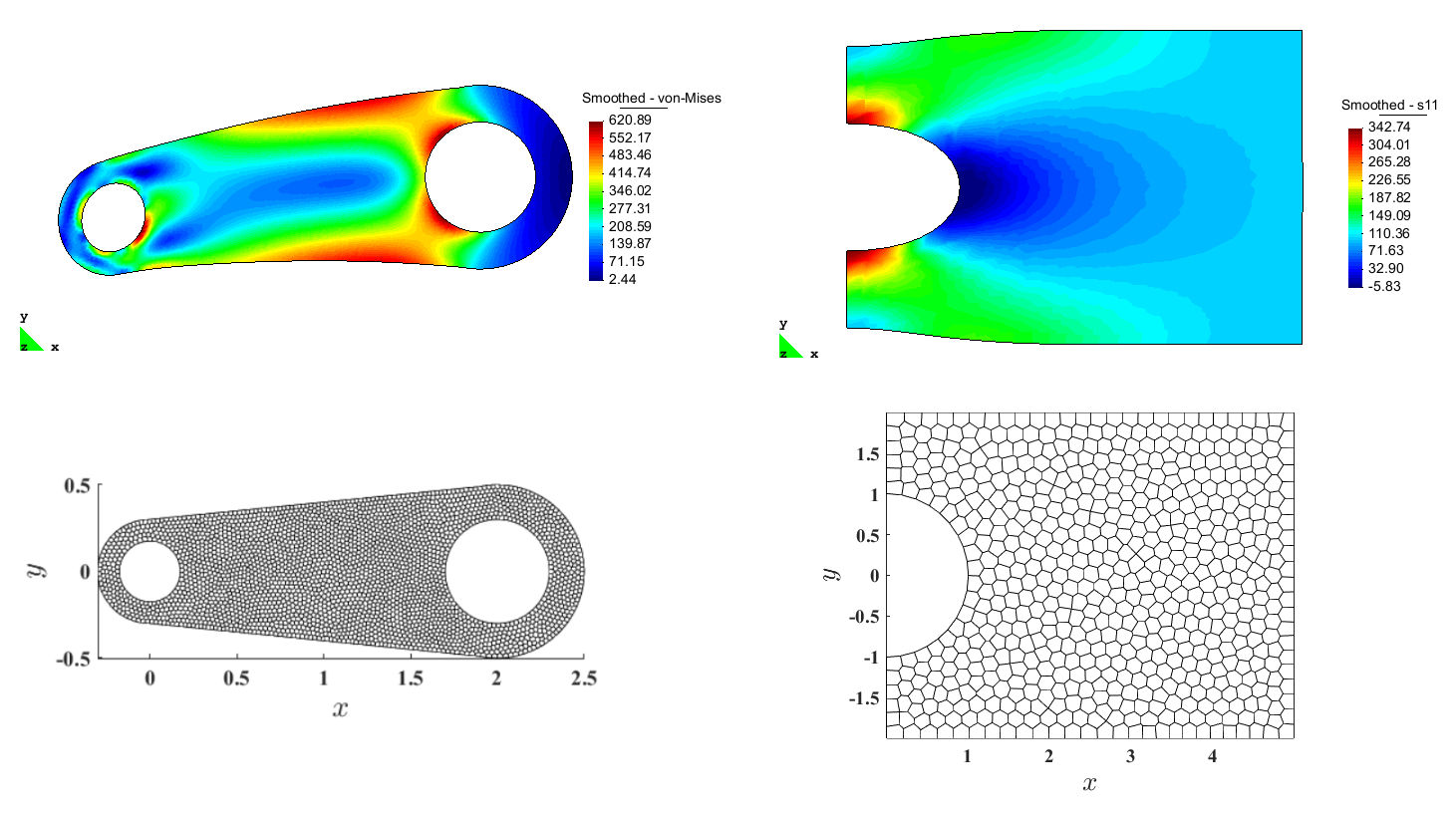
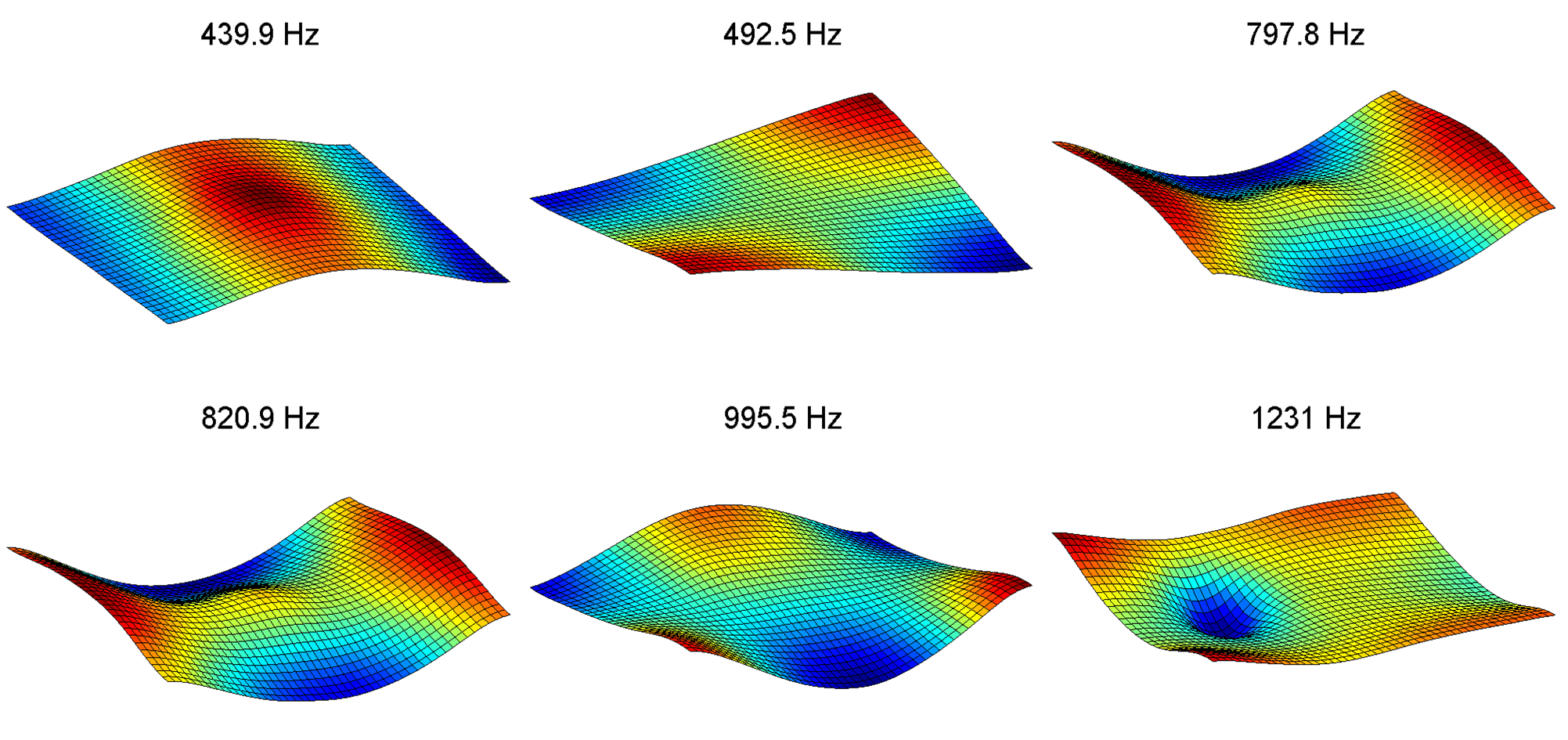
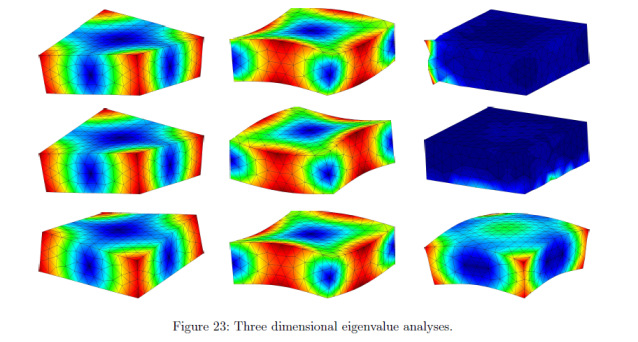
Computer Methods in Applied Mechanics and Engineering Vol. 341, pp. 827-850, 2018 A. Ortiz-Bernardin, P. Köbrich, J. S. Hale, E. Olate-Sanzana, S. P. A. Bordas, S. Natarajan Abstract We introduce a novel meshfree Galerkin method for the solution of Reissner-Mindlin plate problems that is written in terms of the primitive variables only (i.e., rotations and
Read More » Read More
VEMLab: a MATLAB library for the virtual element method Release of VEMLab v2.1 >> From VEMLab v2.0.2 to VEMLab v2.1: Add customized wrench domain (for PolyMesher mesh generator only). Add customized plate with a hole domain (for PolyMesher mesh generator only). Add the following test: “square_plate_with_source2_poisson2d.m” in test folder. Add the following test: “plate_with_hole_linelast2d.m” in
Read More » Read More
VEMLab: a MATLAB library for the virtual element method Release of VEMLab v2.0 From VEMLab v1.0 to VEMLab v2.0: the following features have been added Two-dimensional Poisson problem. Setup of plot and output options in function “plot_and_output_options” located in folder “config”. Additional plotting options (stresses, strains, fluxes and gradients) to MATLAB figures, text files and
Read More » Read More
Paper Accepted for Publication in Entropy V. Meruane, Matias Lasen, E. López Droguett, A. Ortiz-Bernardin, “Modal strain energy-based debonding assessment of sandwich panels using a linear approximation with maximum entropy.” ABSTRACT Sandwich structures are very attractive due to their high strength at a minimum weight, and, therefore, there has been a rapid increase in their
Read More » Read More Entropy Vol. 19, No. 11, pp. 619, 2017 V. Meruane, M. Lasen, E. López Droguett, A. Ortiz-Bernardin Abstract Sandwich structures are very attractive due to their high strength at a minimum weight, and, therefore, there has been a rapid increase in their applications. Nevertheless, these structures may present imperfect bonding or debonding between the skins and
Read More » Read MoreI am looking for highly motivated candidates to fill some postdocs positions in computational solid mechanics in Chile. The ideal candidate must have: a PhD in Mechanical or Civil Engineering, Mathematics or equivalent. experience in developing codes in Matlab, Python or Julia. knowledge of nonlinear finite element methods. publications in ISI journals. Other desirable skills:
Read More » Read More
A talk given by A. Ortiz-Bernardin at POEMS 2017: Workshop on Polytopal Element Methods in Mathematics and Engineering, July 6, 2017, Milan, Italy. Consistent and Stable Meshfree Galerkin Methods Using The Virtual Element Decomposition Alejandro Ortiz-Bernardin Department of Mechanical Engineering, University of Chile Av. Beauchef 851, Santiago, 8370456, Chile aortizb@ing.uchile.cl ABSTRACT In the numerical solution
Read More » Read More
Paper Accepted for Publication in Entropy V. Meruane, P. Véliz, E. López Droguett, A. Ortiz-Bernardin, “Impact location and quantification on an aluminum sandwich panel using principal component analysis and linear approximation with maximum entropy.” ABSTRACT To avoid structural failures it is of critical importance to detect, locate and quantify impact damage as soon as it
Read More » Read More Entropy Vol. 19, No. 4, pp. 137, 2017 V. Meruane, P. Véliz, E. López Droguett, A. Ortiz-Bernardin Abstract To avoid structural failures it is of critical importance to detect, locate and quantify impact damage as soon as it occurs. This can be achieved by impact identification methodologies, which continuously monitor the structure, detecting, locating, and quantifying
Read More » Read More
Paper Accepted for Publication in the International Journal for Numerical Methods in Engineering A. Ortiz-Bernardin, A. Russo, N. Sukumar, “Consistent and stable meshfree Galerkin methods using the virtual element decomposition.” ABSTRACT Over the past two decades, meshfree methods have undergone significant development as a numerical tool to solve partial differential equations (PDEs). In contrast to
Read More » Read More