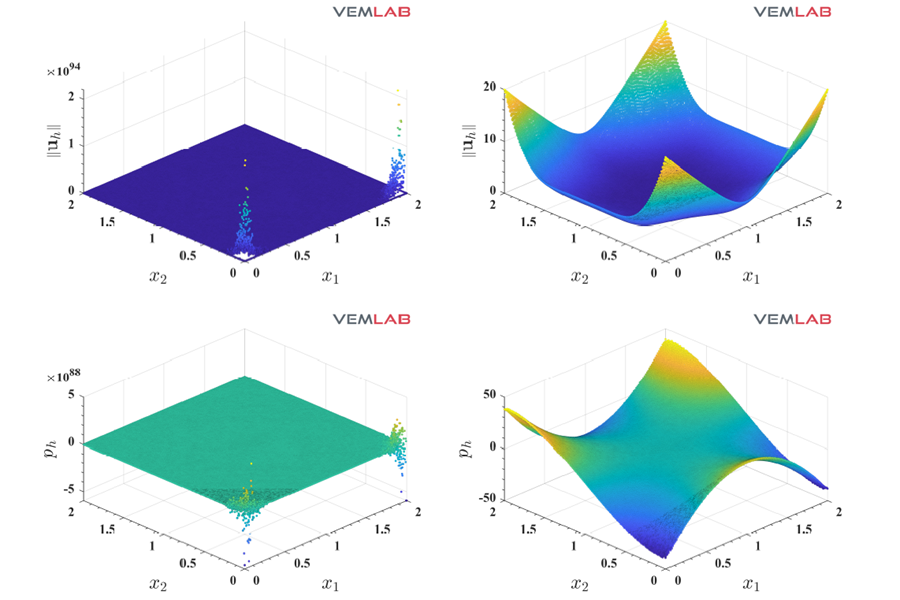
Talk: A Node-Based Uniform Strain Virtual Element Method for Elastic and Inelastic Small Deformation Problems
On June 2, 2022, in Ascona, Switzerland, Professor A. Ortiz-Bernardin gave a talk at CSF Workshop on Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics (CSFWGBC 2022) regarding a
Read More »