Paper Accepted for Publication in the International Journal of Solids and Structures
A. Ortiz-Bernardin, R. Bustamante and K. R. Rajagopal, “A numerical study of elastic bodies that are described by constitutive equations that exhibit limited strains.”
ABSTRACT
Recently, a very general and novel class of implicit bodies has been developed to describe the elastic response of solids. It contains as a special subclass the classical Cauchy and Green elastic bodies. Within the class of such bodies, one can obtain through a rigorous approximation, constitutive relations for the linearized strain as a nonlinear function of the stress. Such an approximation is not possible within classical theories of Cauchy and Green elasticity, where the process of linearization will only lead to the classical linearized elastic body.
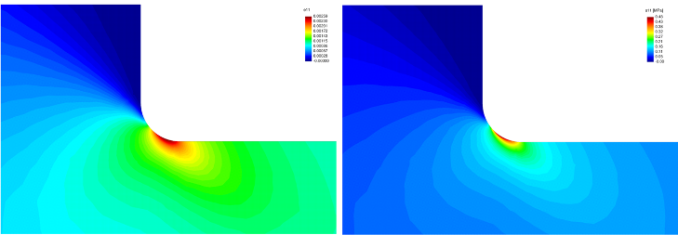
In this paper, we study numerically the states of stress and strain in a finite rectangular plate with an elliptic hole and a stepped flat tension bar with shoulder fillets, within the context of the new class of models for elastic bodies that guarantees that the linearized strain would stay bounded and limited below a value that can be fixed a priori, thereby guaranteeing the validity of the use of the model. This is in contrast to the classical linearized elastic model, wherein the strains can become large enough in the body leading to an obvious inconsistency.