Paper Accepted for Publication in Computer Methods in Applied Mechanics and Engineering
A. Ortiz-Bernardin, M.A. Puso, N. Sukumar, “Improved robustness for nearly-incompressible large deformation meshfree simulations on Delaunay tessellations.”
ABSTRACT
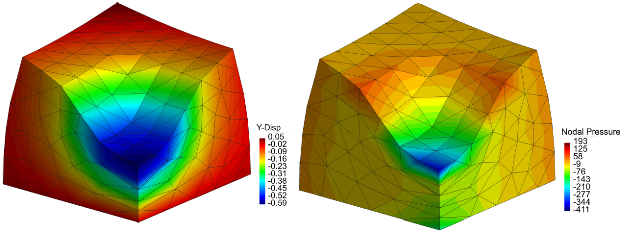
A displacement-based Galerkin meshfree method for large deformation analysis of nearly-incompressible elastic solids is presented. Nodal discretization of the domain is defined by a Delaunay tessellation (three-node triangles and four-node tetrahedra), which is used to form the meshfree basis functions and to numerically integrate the weak form integrals. In the proposed approach for nearly-incompressible solids, a volume-averaged nodal projection operator is constructed to average the dilatational constraint at a node from the displacement field of surrounding nodes. The nodal dilatational constraint is then projected onto the linear approximation space. The displacement field is constructed on the linear space and enriched with bubble-like meshfree basis functions for stability. The new procedure leads to a displacement-based formulation that is similar to F-bar methodologies in finite elements and isogeometric analysis. We adopt maximum-entropy meshfree basis functions, and the performance of the meshfree method is demonstrated on benchmark problems using structured and unstructured background meshes in two and three dimensions. The nonlinear simulations reveal that the proposed methodology provides improved robustness for nearly-incompressible large deformation analysis on Delaunay meshes.