A nodal integration scheme for meshfree Galerkin methods using the virtual element decomposition
- Post by: alejandro
- December 18, 2019
- Comments off
International Journal for Numerical Methods in Engineering
Vol. 121, No. 10, pp. 2174-2205, 2020
R. Silva-Valenzuela, A. Ortiz-Bernardin, N. Sukumar, E. Artioli, N. Hitschfeld-Kahler
Abstract
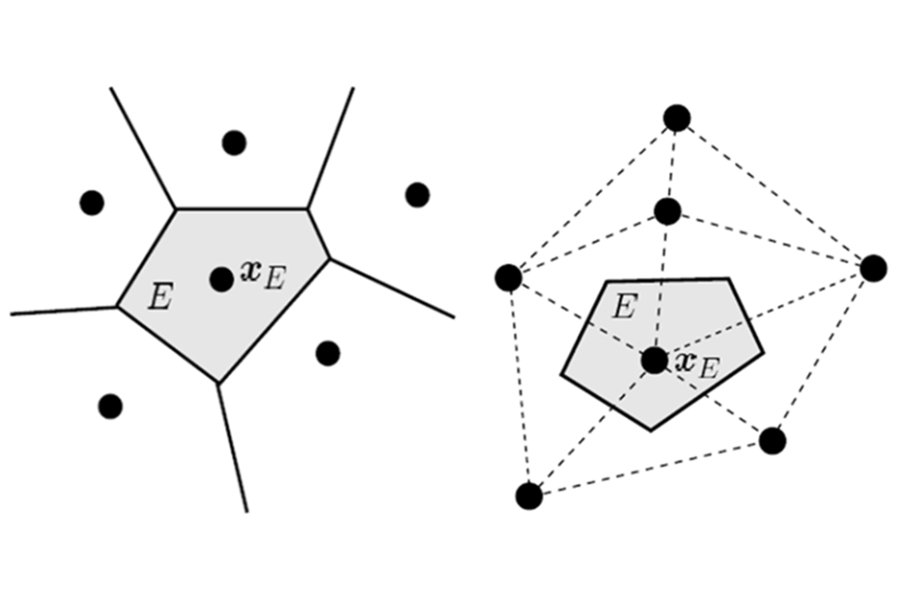
In this paper, we present a novel nodal integration scheme for meshfree Galerkin methods that draws on the mathematical framework of the virtual element method. We adopt linear maximum-entropy basis functions for the discretization of field variables, although the proposed scheme is applicable to any linear meshfree approximant. In our approach, the weak form integrals are nodally integrated using nodal representative cells that carry the nodal displacements and state variables such as strains and stresses. The nodal integration is performed using the virtual element decomposition, wherein the bilinear form is decomposed into a consistency part and a stability part that ensure consistency and stability of the method. The performance of the proposed nodal integration scheme is assessed through benchmark problems in linear and nonlinear analysis of solids for small displacements and small-strain kinematics. Numerical results are presented for linear elastostatics and linear elastodynamics, and viscoelasticity. We demonstrate that the proposed nodally integrated meshfree method is accurate, converges optimally, and is more reliable and robust than a standard cell-based Gauss integrated meshfree method.
Keywords: nodal integration, meshfree Galerkin methods, maximum-entropy approximants, virtual element method, patch test, stability.
Original Journal Article: https://doi.org/10.1002/nme.6304
Personal preprint:
NOTICE: this is the author’s version of a work that was accepted for publication. Changes resulting from the publishing process, such as peer review, editing, corrections, structural formatting, and other quality control mechanisms may not be reflected in this document.
