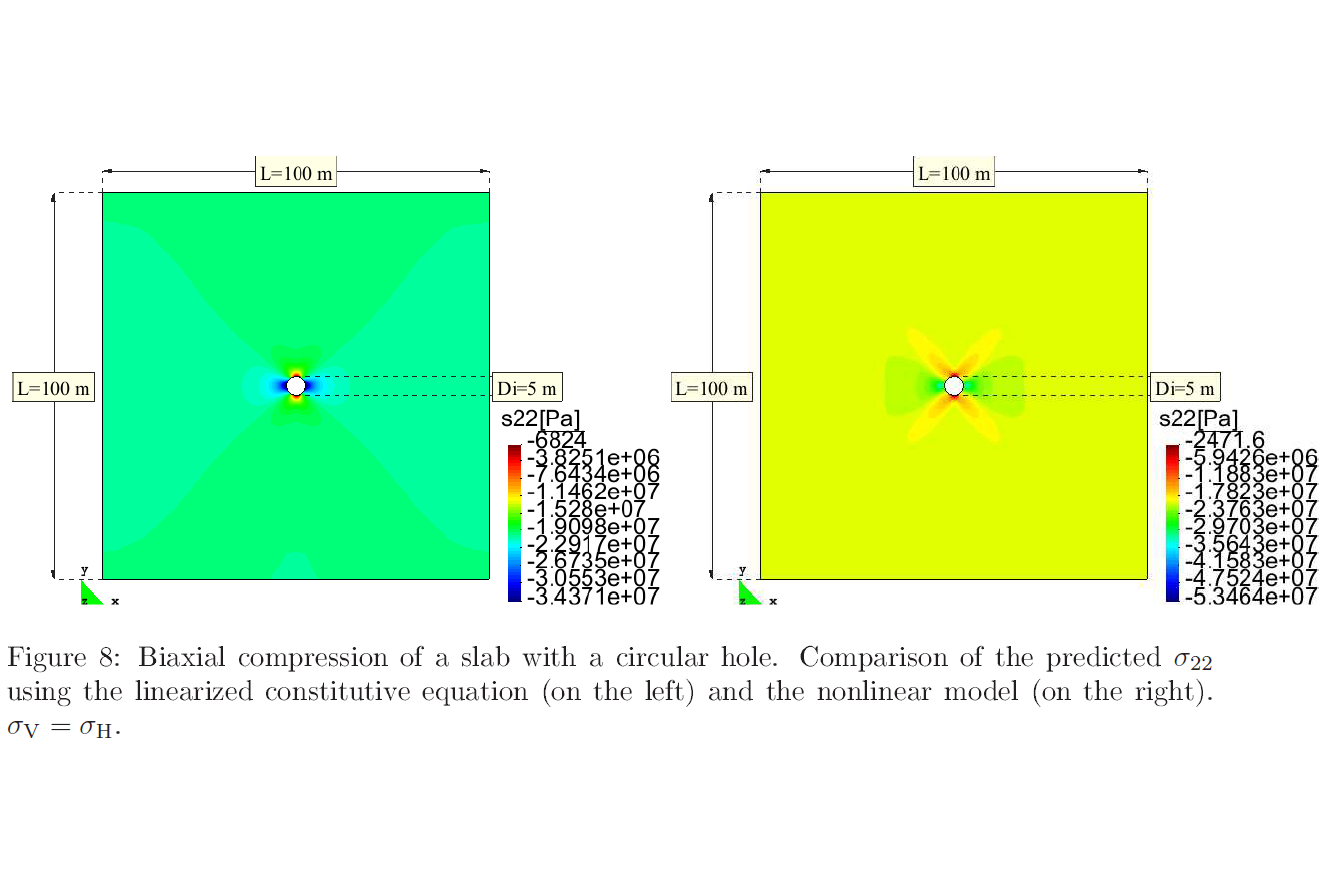
Accepted Paper: A novel nonlinear constitutive model for rock: numerical assessment and benchmarking
Paper Accepted for Publication in Applications in Engineering Science R. Bustamante, S. Montero, A. Ortiz-Bernardin, “A novel nonlinear constitutive model for rock: numerical assessment and benchmarking” ABSTRACT In this article,
Read More »