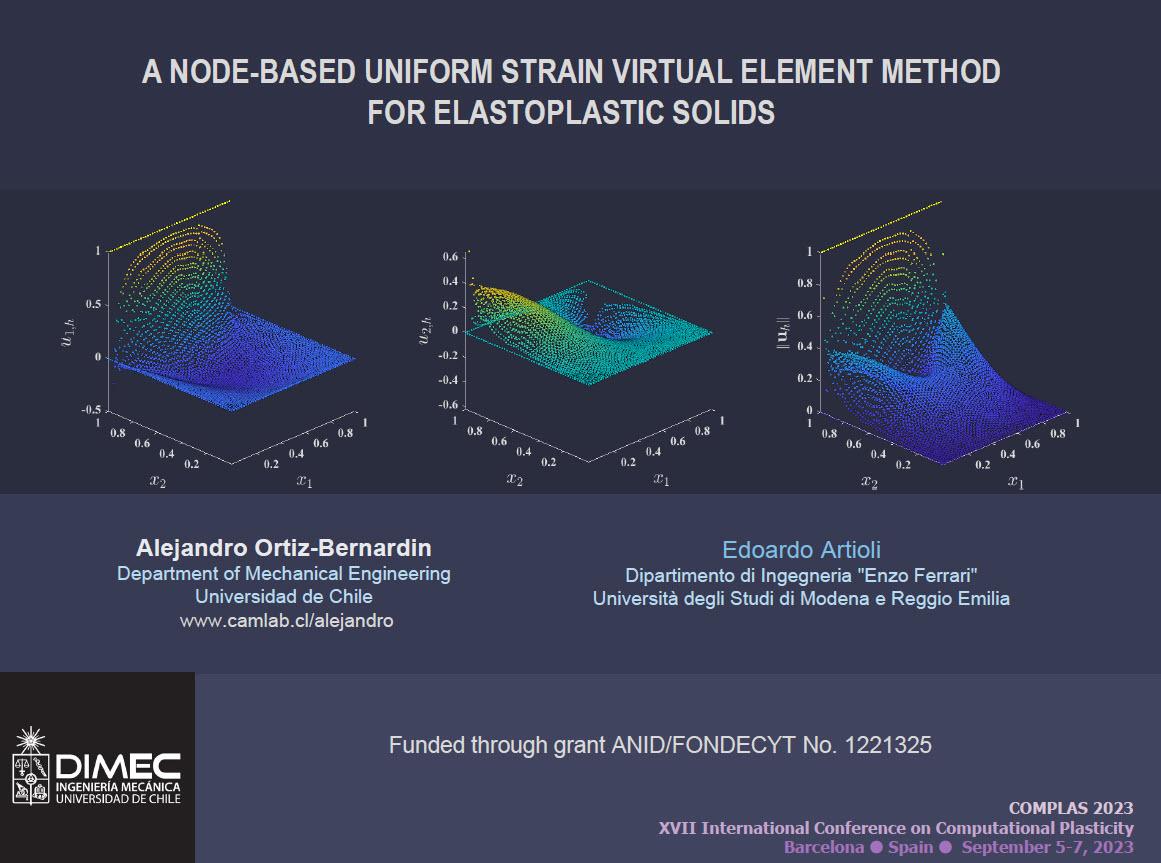
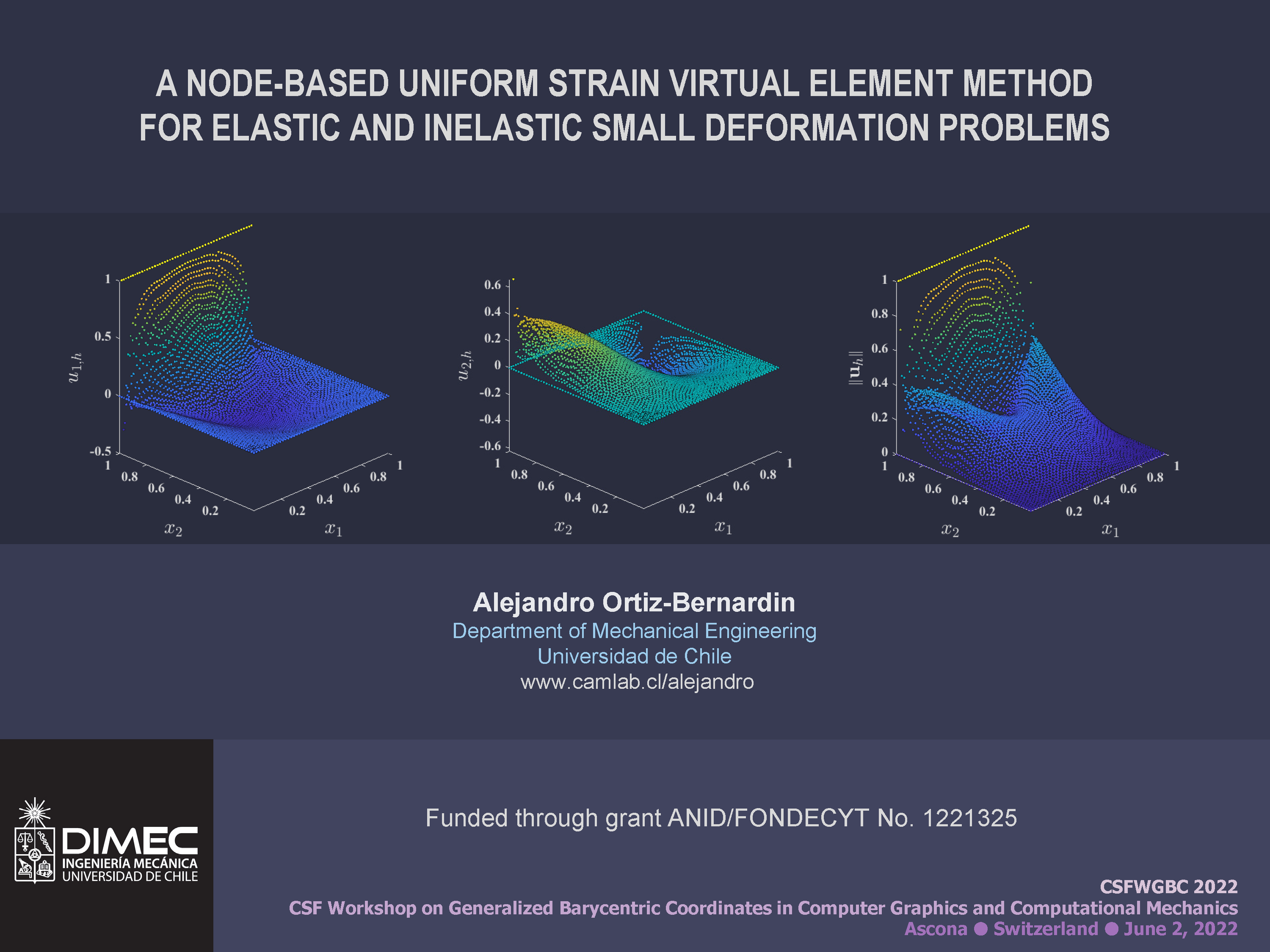
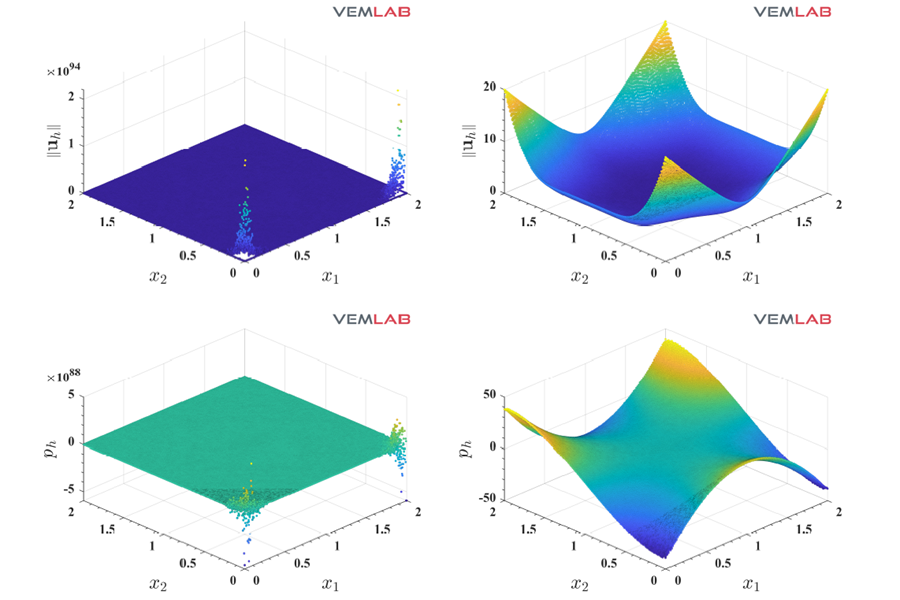
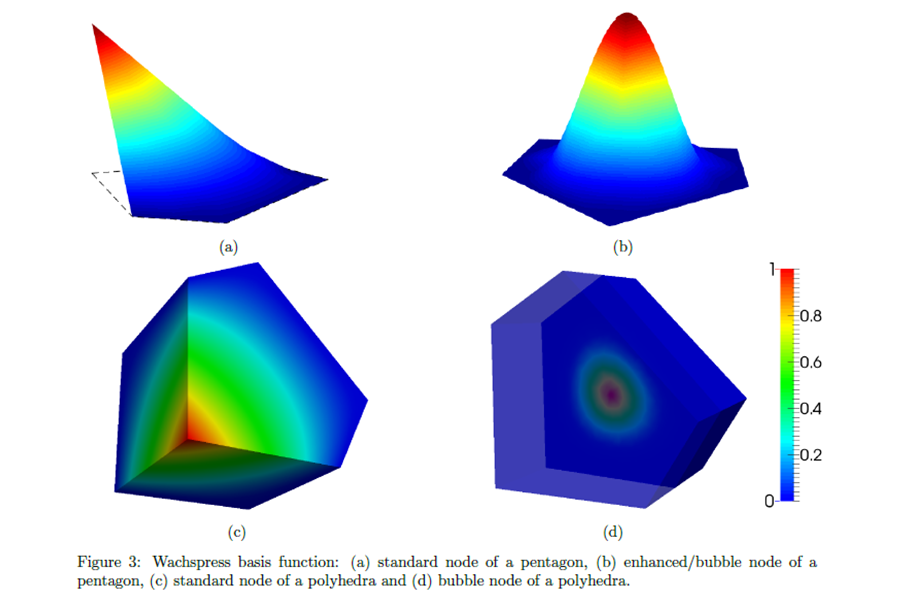
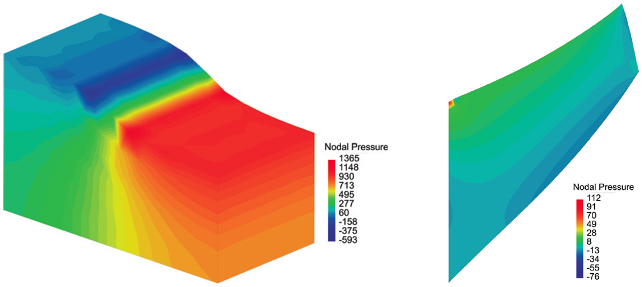
Talk: A Node-Based Uniform Strain Virtual Element Method for Elastoplastic Solids
On September 6, 2023, in Barcelona, Spain, Professor A. Ortiz-Bernardin gave a talk at COMPLAS 2023 regarding a combination between nodal integration techniques and the virtual element method with applications
Read More »