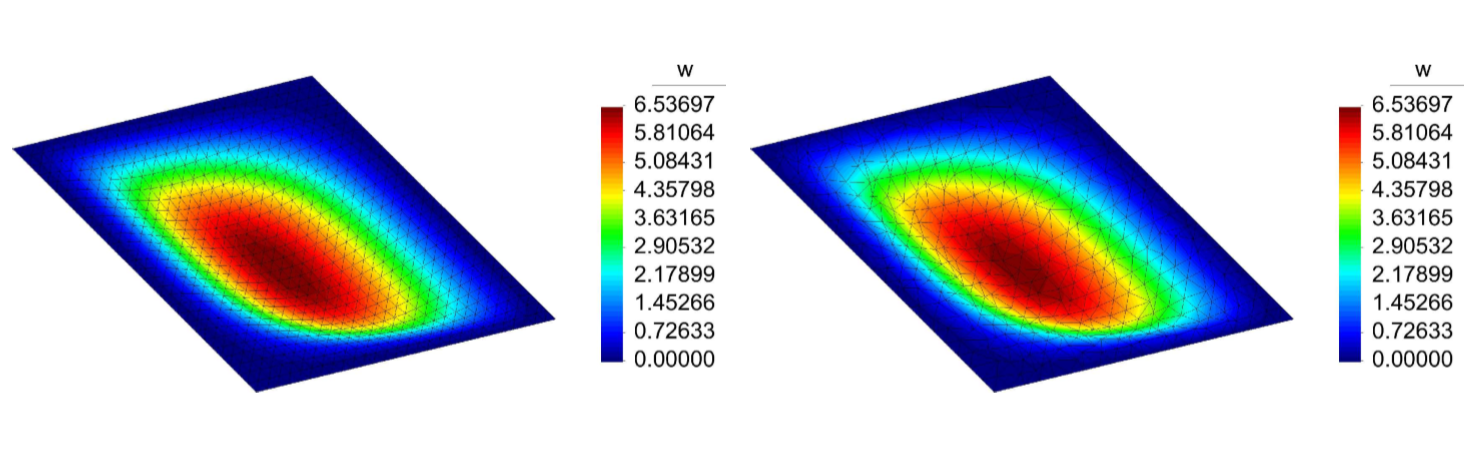
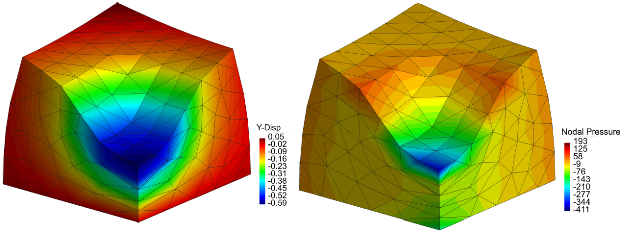
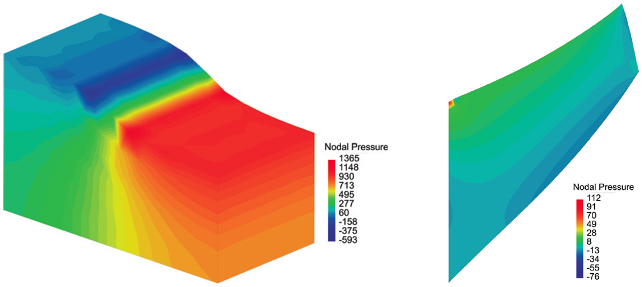
Accepted Paper: A volume-averaged nodal projection method for the Reissner-Mindlin plate model
Paper Accepted for Publication in Computer Methods in Applied Mechanics and Engineering A. Ortiz-Bernardin, Philip Köbrich, Jack S. Hale, Edgardo Olate-Sanzana, Stéphane P. A. Bordas, Sundararajan Natarajan, “A volume-averaged nodal projection
Read More »