Latest News
A Node-Based Uniform Strain Virtual Element Method for Elastoplastic Solids
A talk given by A. Ortiz-Bernardin at COMPLAS 2023, September 6, 2023, Barcelona, Spain. A NODE-BASED UNIFORM STRAIN VIRTUAL ELEMENT…
A Node-Based Uniform Strain Virtual Element Method for Elastic and Inelastic Small Deformation Problems
A talk given by A. Ortiz-Bernardin at CSFWGBC 2022, June 2, 2022, Ascona, Switzerland. A NODE-BASED UNIFORM STRAIN VIRTUAL ELEMENT…
Accepted Paper: A node-based uniform strain virtual element method for compressible and nearly incompressible elasticity
Paper Accepted for Publication in International Journal for Numerical Methods in Engineering A. Ortiz-Bernardin, R. Silva-Valenzuela, S. Salinas-Fernández, N. Hitschfeld-Kahler, S. Luza, B. Rebolledo, "A node-based…
VEMLAB
The free and open-source library for the Virtual Element Method
Latest Journal Articles
Some of our latest research efforts are tailored to devise new nodal integration techniques by combining meshfree Galerkin methods with the relatively new numerical technology offered by the Virtual Element Method. Nodal integration schemes formulated in this manner are stable and convergent by construction. In this approach, state variables such as strains, stresses, and other internal variables in nonlinear computations can be stored at the nodes just like the displacements.
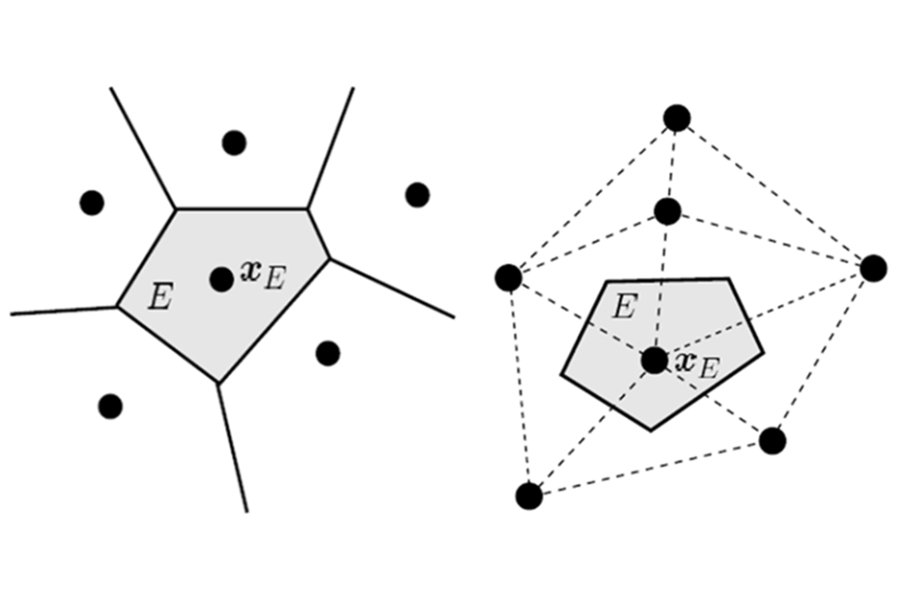
Some nodal cells used in nodal integration.
