Veamy: an extensible object-oriented C++ library for the virtual element method
- Post by: alejandro
- December 24, 2018
- Comments off
Numerical Algorithms
Vol. 82, pp. 1189-1220, 2019
A. Ortiz-Bernardin, C. Alvarez, N. Hitschfeld-Kahler, A. Russo, R. Silva-Valenzuela, E. Olate-Sanzana
Abstract
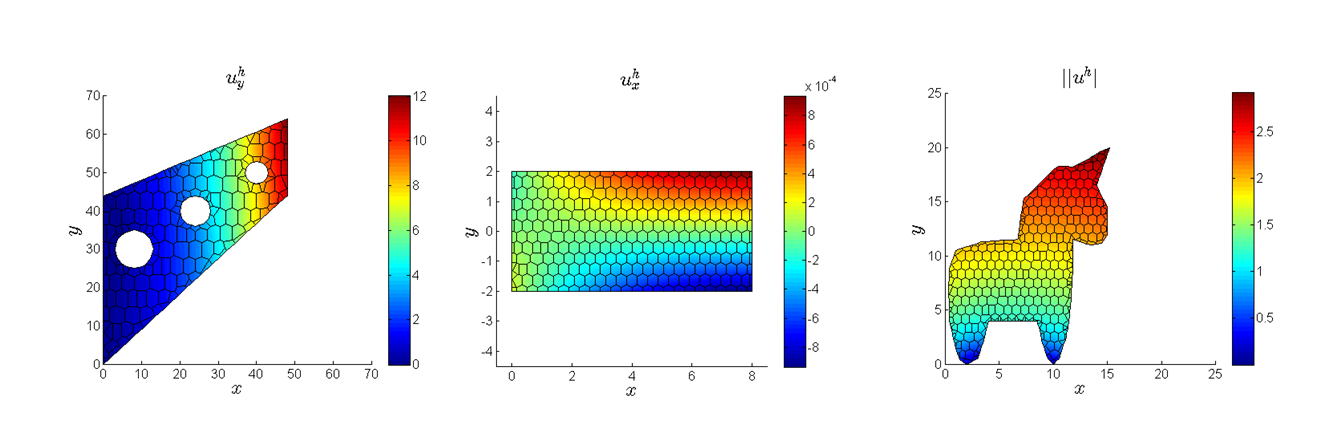
This paper summarizes the development of Veamy, an object-oriented C++ library for the virtual element method (VEM) on general polygonal meshes, whose modular design is focused on its extensibility. The linear elastostatic and Poisson problems in two dimensions have been chosen as the starting stage for the development of this library. The theory of the VEM, upon which Veamy is built, is presented using a notation and a terminology that resemble the language of the finite element method (FEM) in engineering analysis. Several examples are provided to demonstrate the usage of Veamy, and in particular, one of them features the interaction between Veamy and the polygonal mesh generator PolyMesher. A computational performance comparison between VEM and FEM is also conducted. Veamy is free and open source software.
Keywords: virtual element method, polygonal meshes, object-oriented programming , C++.
Original Journal Article: https://doi.org/10.1007/s11075-018-00651-0
Personal preprint:
NOTICE: this is the author’s version of a work that was accepted for publication. Changes resulting from the publishing process, such as peer review, editing, corrections, structural formatting, and other quality control mechanisms may not be reflected in this document.
