meshfree Galerkin methods

A Meshfree Nodal Integration Method for Elastic and Elastoplastic Applications Using The Virtual Element Decomposition

December 23, 2019
Comments off

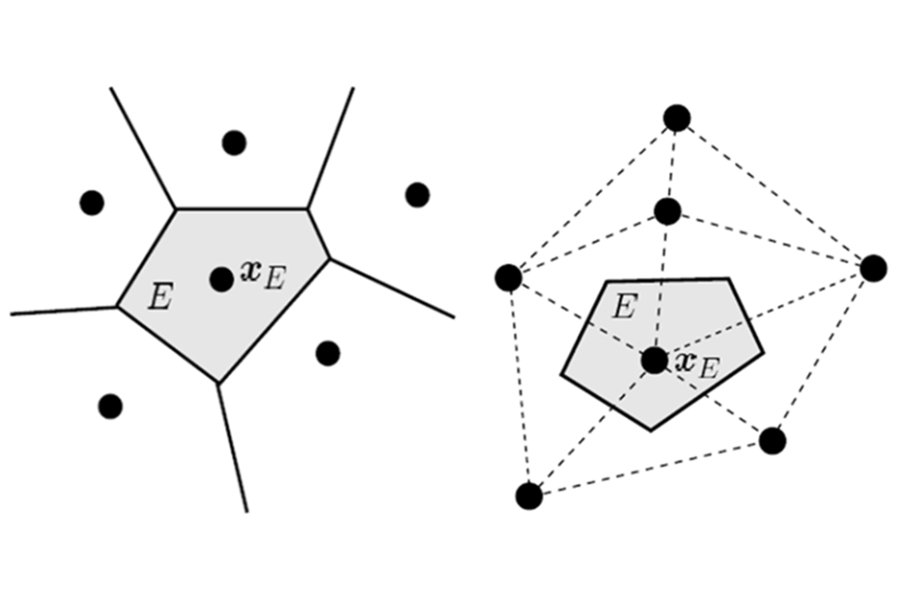
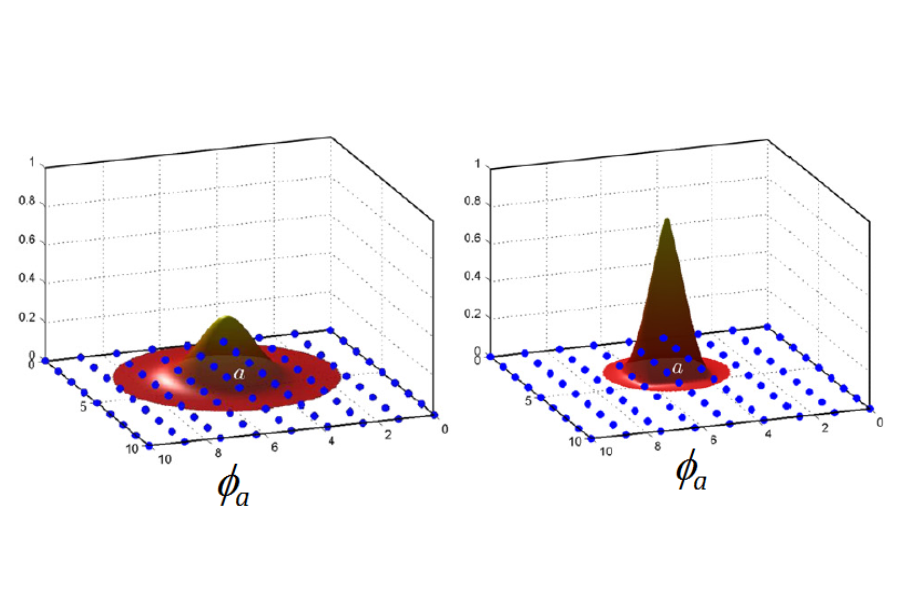
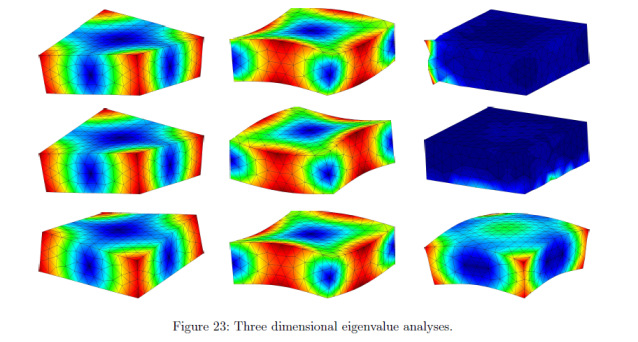
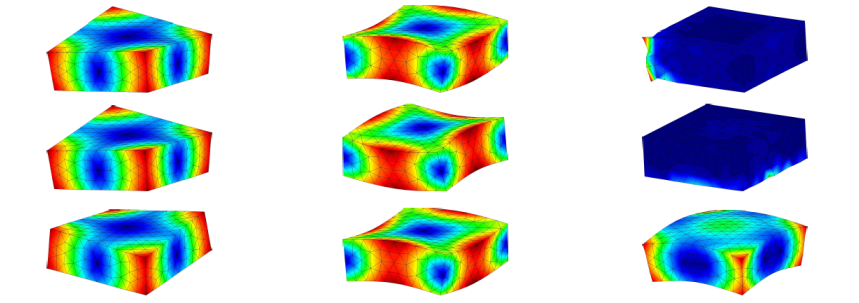
A talk given by A. Ortiz-Bernardin at COMPLAS 2019, September 3, 2019, Barcelona, Spain. A MESHFREE NODAL INTEGRATION METHOD FOR ELASTIC AND ELASTOPLASTIC APPLICATIONS USING THE VIRTUAL ELEMENT DECOMPOSITION A. ORTIZ-BERNARDIN a, E. ARTIOLI b, AND R. SILVA-VALENZUELA a Abstract. In meshfree Galerkin methods to solve partial differential equations, a cloud of nodes is used

Read More » Read More

Sample of two-dimensional nodal cells used in nodal integration

Accepted Paper: A nodal integration scheme for meshfree Galerkin methods using the virtual element decomposition

December 18, 2019
Comments off

Paper Accepted for Publication in International Journal for Numerical Methods in Engineering R. Silva-Valenzuela, A. Ortiz-Bernardin, N. Sukumar, E. Artioli, N. Hitschfeld-Kahler, “A nodal integration scheme for meshfree Galerkin methods using the virtual element decomposition” ABSTRACT In this paper, we present a novel nodal integration scheme for meshfree Galerkin methods that draws on the mathematical

Read More » Read More

A nodal integration scheme for meshfree Galerkin methods using the virtual element decomposition

December 18, 2019
Comments off

International Journal for Numerical Methods in Engineering Vol. 121, No. 10, pp. 2174-2205, 2020 R. Silva-Valenzuela, A. Ortiz-Bernardin, N. Sukumar, E. Artioli, N. Hitschfeld-Kahler Abstract In this paper, we present a novel nodal integration scheme for meshfree Galerkin methods that draws on the mathematical framework of the virtual element method. We adopt linear maximum-entropy basis

Read More » Read More

Enhancing the robustness of meshfree Galerkin methods for solid mechanics simulations using the virtual element decomposition

October 11, 2018
Comments off

2018 – 2021 Principal Investigator: Alejandro Ortiz-Bernardin. Project funded by CONICYT-FONDECYT (Grant Nº 1181192) Meshfree methods have several attributes that make them attractive for simulation in mechanics. Two important ones are summarized as follows. The meshfree approximation is independent of the definition of a finite element mesh — the approximation is constructed based solely on nodal locations.

Read More » Read More

Accepted Paper: Consistent and stable meshfree Galerkin methods using the virtual element decomposition

January 24, 2017
Comments off

Paper Accepted for Publication in the International Journal for Numerical Methods in Engineering A. Ortiz-Bernardin, A. Russo, N. Sukumar, “Consistent and stable meshfree Galerkin methods using the virtual element decomposition.” ABSTRACT Over the past two decades, meshfree methods have undergone significant development as a numerical tool to solve partial differential equations (PDEs). In contrast to

Read More » Read More

Consistent and stable meshfree Galerkin methods using the virtual element decomposition

January 24, 2017
Comments off

International Journal for Numerical Methods in Engineering Vol. 112, No. 7, pp 655-684, 2017 A. Ortiz-Bernardin, A. Russo, N. Sukumar Abstract Over the past two decades, meshfree methods have undergone significant development as a numerical tool to solve partial differential equations (PDEs). In contrast to finite elements, the basis functions in meshfree methods are smooth

Read More » Read More

Paper Submitted: Consistent and stable meshfree Galerkin methods using the virtual element decomposition

November 7, 2016
Comments off

A. Ortiz-Bernardin, A. Russo, N. Sukumar, “Consistent and stable meshfree Galerkin methods using the virtual element decomposition,” submitted. ABSTRACT Over the past two decades, meshfree methods have undergone significant development as a numerical tool to solve partial differential equations (PDEs). In contrast to finite elements, the basis functions in meshfree method are smooth (nonpolynomial functions),

Read More » Read More