2012 – 2015
Principal Investigator: Roger Bustamante.
Co-Investigator: Alejandro Ortiz-Bernardin.
Project funded by CONICYT-FONDECYT (Grant Nº 1120011)
In the classical theory of continuum mechanics there are two concepts which are considered
particularly important, namely stresses and strains. Even though, from an intuitive point of
view, we would say that strains are ‘caused’ due to the presence of stresses in a body, when
proposing constitutive laws for these two quantities, it is normally assumed that stresses are
expressed as ‘functions’ of strains.
In the case of elastic bodies, recognizing that the above assumption would be too
restrictive to model the behavior of all bodies that can be considered as elastic, recently it has
been proposed some implicit constitutive laws, where with stresses and strains we define a
mathematical relation, from where in general stresses cannot be obtained as functions of
strains. Special cases of the above implicit laws are not only the Cauchy and Green elastic
bodies, but also elastic bodies for which strains are in general non-linear functions of stresses.
Of particular interest is the problem when we assume that stresses can be arbitrarily ‘large’
but strains remain bounded, where it has been shown that to express strains as functions of
stresses is the correct way to relate these two quantities from the rational point of view.
Applications of that subclass of constitutive law lie, for example, in fracture mechanics.
In this research proposal we are interested in assessing in detail these new constitutive
laws, with particular interests for the case we have a nonlinear behavior for the material and
strains are expressed as functions of stresses. We are interested in two problems, which we
classify in terms of the norm of the displacement gradient: considering arbitrarily large
displacement gradient, and considering small displacement gradient.
In order to have an idea of how these new constitutive laws behave, and what kind of
problems can be addressed in a ‘better’ way with these laws, we will solve several different
boundary value problems, using both analytical and numerical methods.
For the analytical methods we will use the semi-inverse method, where we will prescribe
some known deformations, and for some specific constitutive functions we will compute the
stresses, which have to satisfy the equilibrium equations. In the case of considering small
displacement gradient, we will be particularly interested in studying some examples of
constitutive functions for which we have a strain limiting behavior.
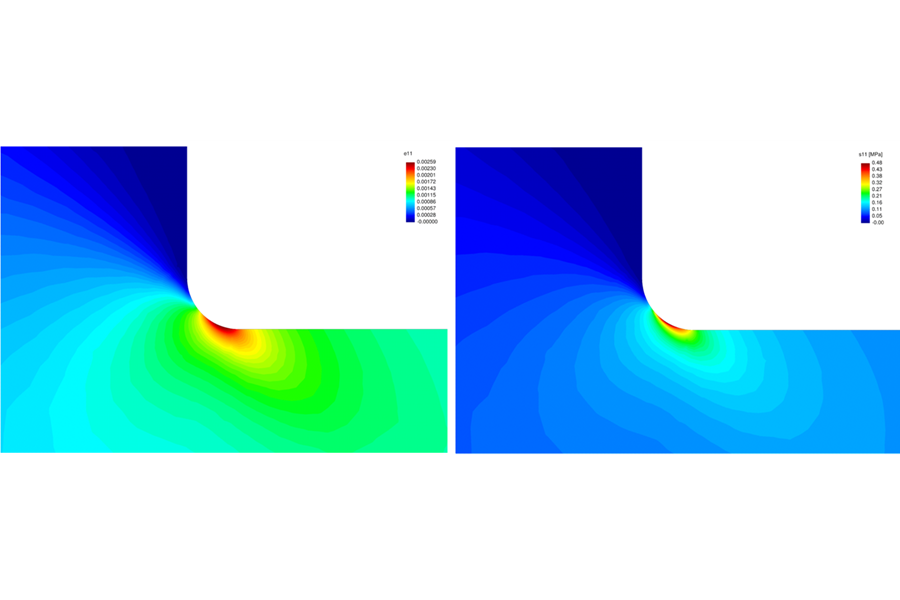
In the case of the numerical solutions, we will use the finite element method,
considering first a classical nonlinear formulation based in the displacement field as the main
variable, and then we will consider a mixed formulation with the displacement field and the
stress tensor as the variables to be directly determined through interpolation.
Some other problems will be treated, such as the study of constraints for this new class
of constitutive laws, and how they are related with the classical method they have been
incorporated in continuum mechanics. As well as this, we will explore a possible application of
these constitutive laws to model the mechanical behavior of residually stressed bodies.
Finally, for the case of small displacement gradient, we will do a stability analysis for some
problems based on an incremental formulation and the use of the stress vector potential.
Publications