2016 – 2020
Principal Investigator: Roger Bustamante.
Co-Investigator: Alejandro Ortiz-Bernardin.
Project funded by CONICYT-FONDECYT (Grant Nº 1160030)
Geomaterials such as rock and soil can show a plethora of nonlinear phenomena regarding their mechanical behaviour, such as: hysteresis (i.e., dependency of the mechanical properties in the load history), nonlinear relations between stresses and strains (even in the case of considering small strains), complex failure mechanisms that depend among other things on the pressure applied on the material, etc.
Depending on the specific applications (and in particular depending on the time scale and the magnitude of the external applied loads), in the mathematical modelling of the mechanical behaviour of such geomaterials, it is assumed either that they behave as elastic or ‘elasto-plastic’ bodies. By an elastic body we mean a body that does not dissipate mechanical work into heat, whereas by ‘elasto-plastic’ body we mean a body where there is dissipation of mechanical work into heat. In any of these two cases the classical approach that has been considered to model the behaviour of such bodies, has been to assume that the stresses are functions of the strains. However, recently some new classes of constitutive relations have been proposed, where the stresses and strains are expressed in terms of implicit relations, where in general it is not possible to express the stresses as functions of the strains. Such constitutive relations have been useful to study, for example, the problem of an elastic body where strains are small but the behaviour is nonlinear. In the case of a body that dissipate work into heat, it has been shown that such implicit constitutive relations expand greatly the phenomena that can be studied, and in particular, by using such relations it is not necessary to use some concepts such as ‘plastic deformations’ (as a basic ingredient for the model), which in the literature has been a topic that has created some controversies from the theoretical point of view.
In this proposal we aim to use such implicit constitutive relations in the case of modelling the behaviour of geomaterials, specifically in the mathematical modelling of the mechanical behaviour of rock. Both large and infinitesimal deformations will be considered, as well as this, in the case of infinitesimal deformations, the bodies will be assumed to be either elastic or dissipative (in the sense of dissipating mechanical work into heat).
This research is divided in three main phases:
- First, some theoretical issues regarding these implicit constitutive relations will be addressed, such as to propose some constitutive inequalities, to solve some simple boundary value problems (using the semi-inverse method from the nonlinear theory of elasticity), and to propose some specific expressions for the constitutive relations using the experimental data available in the literature.
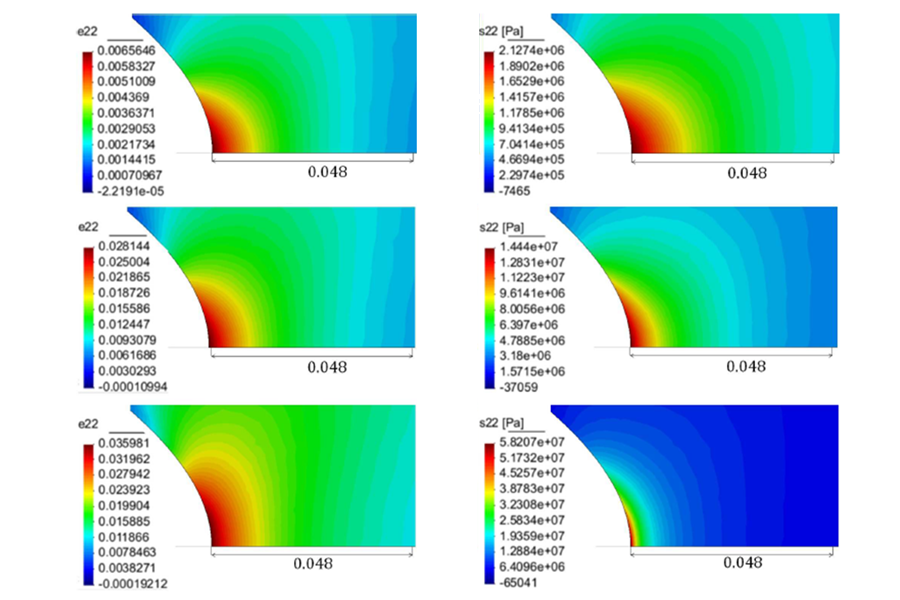
- In a second stage, a finite element code will be modified in order to use these new constitutive relations, and some more complex two-dimensional boundary value problems will be solved using such code.
- In the last stage, these implicit relations will be used to model, in a simplified manner, the process of caving used in underground mining, and also the propagation of seismic waves considering a simple model of the earth crush.
In the case of some of the simple boundary value problems mentioned previously, the rock will be assumed to be ‘intact’, i.e., no faults or joints will be present; whereas for some of the two-dimensional problems, and in particular in the application to the modelling of caving and wave propagation, some of such discontinuities will be incorporated into the models.
Publications